Mining Ring Systems in Molecules for Fun and Profit

I've been a longtime fan of Peter Ertl's work on identifying and classifying the ring systems in molecules.  I wanted a Python implementation for some of my work, so I coded something similar in spirit to what Peter has published.  In this post, I begin by highlighting some of Peter's papers and showing some interesting analyses that can be performed with a tool for extracting ring systems.   After introducing the motivation for the work, we get into the geeky details and explore one approach to identifying ring systems.  Finally, we will look at a simple application of the method and explore the ring systems in marketed drugs.  In an upcoming post, I'll show another, more interesting, application of the method.  The code accompanying this post is in a Jupyter notebook on GitHub.   In addition, the core code for extracting ring systems from molecules has been incorporated into the latest version of my pip installable useful_rdkit_utils package.  I've also incorporated this notebook into the Practical Cheminformatics Tutorials.

A Bit of Background

For those less familiar with Peter Ertl's work, here's a brief primer.  

In a 2006 paper, Peter and his coworkers analyzed a set of 150,000 bioactive molecules from the World Drug Index (WDI) and the MDL Drug Data Report (MDDR).   Based on this analysis, they found that their bioactive molecules contained only 780 distinct, simple aromatic (SA) ring systems. These SA ring systems were defined as systems consisting of two or three rings with five or six heavy atoms in each ring.  To evaluate a broader set of ring systems, the authors used a set of 14 ring templates and 8 chemical building blocks, consisting of 3 to 4 heavy atoms, to exhaustively enumerate a set of almost 600,000 elaborated ring systems.  A set of topological and quantum chemical descriptors were calculated for each molecule.  These descriptors were then used to train a self-organizing map (SOM), which projected the molecules into a two-dimensional grid where similar molecules were close together in the 2D space.  For more information on self-organizing maps, please see this post, this one, and this tutorial.  The enumerated ring systems near bioactive rings in the SOM space were deemed "interesting," and commercially available molecules containing these ring systems were used to augment a screening collection.

Ertl, P., Jelfs, S., Mühlbacher, J., Schuffenhauer, A., & Selzer, P. (2006). Quest for the rings. In silico exploration of ring universe to identify novel bioactive heteroaromatic scaffolds. Journal of Medicinal Chemistry, 49(15), 4568-4573.

In a 2012 paper, Peter showed how molecular descriptors can be used to characterize ring systems and perform similarity searches. In this application, ring systems are represented using several characteristics, including shape, electrostatics, and pharmacophore features. Ring systems were subsequently compared based on the RMSD between descriptor vectors. 

Ertl, P. (2012). Database of bioactive ring systems with calculated properties and its use in bioisosteric design and scaffold hopping. Bioorganic & Medicinal Chemistry, 20(18), 5436-5442.

A 2021 paper extended Peter's previous work and led to the development of a web tool for navigating scaffolds found in the ChEMBL and ZINC databases.  A set of 40,000 rings was collected from these two databases, and the relative occurrence of rings between the two databases was used to define a set of "bioactive" rings.  Descriptors were calculated for the rings, and dimensionality reduction (PCA) was used to plot the ring descriptors in two dimensions.  The embedding space produced by the PCA was then binned into hexagonal sections containing similar rings.  The output of this analysis is available in a web tool called Magic Rings. 

Ertl, P. (2021). Magic Rings: Navigation in the ring chemical space guided by the bioactive rings. Journal of Chemical Information and Modeling, 62(9), 2164-2170.

In a 2022 paper, Peter and coworkers used data from the ChEMBL database to identify sets of ring systems with similar biological activity.  The analysis began with the extraction of chemical series from datasets associated with papers in ChEMBL.  Each series was then evaluated to find pairs of compounds that only differed by a single ring system.  These pairs and the associated differences in biological activity were tabulated. and pairs that occurred at least 5 times were retained.   By aggregating these pairs, the authors defined sets of bioequivalent replacements for ring systems commonly used in medicinal chemistry.  These replacements can be accessed through a user-friendly web tool known as the Ring Replacement Recommender. 

Ertl, P., Altmann, E., Racine, S., & Lewis, R. (2022). Ring replacement recommender: Ring modifications for improving biological activity. European Journal of Medicinal Chemistry, 114483.

Of course, Peter isn't the only person to publish analyses of ring systems.  There have been numerous other papers describing the ring systems in drugs and natural products. 

Bemis, G. W., & Murcko, M. A. (1996). The properties of known drugs. 1. Molecular frameworks. Journal of Medicinal Chemistry, 39(15), 2887-2893.

Taylor, R. D., MacCoss, M., & Lawson, A. D. (2014). Rings in drugs: Miniperspective. Journal of Medicinal Chemistry, 57(14), 5845-5859.

Shearer, J., Castro, J. L., Lawson, A. D., MacCoss, M., & Taylor, R. D. (2022). Rings in clinical trials and drugs: Present and future. Journal of Medicinal Chemistry, 65(13), 8699-8712.

Aldeghi, M., Malhotra, S., Selwood, D. L., & Chan, A. W. E. (2014). Two- and three-dimensional rings in drugs. Chemical Biology & Drug Design, 83(4), 450-461.

Chen, Y., Rosenkranz, C., Hirte, S., & Kirchmair, J. (2022). Ring systems in natural products: structural diversity, physicochemical properties, and coverage by synthetic compounds. Natural Product Reports, 39(8), 1544-1556.

What is a Ring System? 

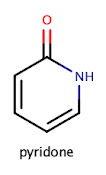
Now that we've looked at some of the work people have done with ring systems let's get into a bit more detail.  At a simple level, we can define a ring system as the atoms within a molecule that are contained in cycles.  Unfortunately, this definition quickly collapses when considering a system such as pyridone.  

If we remove the carbonyl oxygen, we fundamentally change the ring system.  In most definitions of ring systems, such as those proposed by Bemis and Murcko, exocyclic double bonds are considered to be part of the ring system.  At this point, the astute reader may be thinking, "ring systems, why not just use Bemis-Murcko scaffolds?".  There is a subtle distinction here.  Bemis-Murcko scaffolds include rings and linkers.  As an example, consider the molecule on the left and its corresponding Bemis-Murcko scaffold on the right.   Note that the Bemis-Murcko scaffold contains a linker between two ring systems. 

Extracting ring systems from the molecule above on the left is a little tricky.  We don't want to remove the exocyclic double bonds and disrupt the rings.  As such, we'll mark the exocyclic double bonds as "preserved" and cleave the remaining non-ring bonds.   This will leave us with two ring systems.   The section below provides a step-by-step walkthrough of the algorithm I used to extract ring systems. 

An Algorithm to Identify Ring Systems

We begin by identifying exocyclic double bonds connected to rings.  As we define ring systems, we want to preserve these bonds as part of a ring.  We can identify the exocyclic double bonds with this SMARTS pattern, which defines a carbon or sulfur atom in a ring connected to a non-ring oxygen, sulfur, carbon, or nitrogen.

[#6R,#18R]=[OR0,SR0,CR0,NR0]

These bonds are tagged as "protected" and won't be cleaved in subsequent steps.  In the figure below, we see these bonds highlighted in red. 

In the next step,  single bonds not in rings are cleaved.   In this application, we first loop over the bonds in the molecule and collect the bonds that are not in rings and not labeled as "protected."  This list of bonds is then passed to the RDKit's FragmentOnBonds function.   For more information on this function, check out Andrew Dalke's blog post from 2016.  

After applying FragmentOnBonds, we have a set of fragments with dummy atoms attached at the cleavage points.  The labels on the fragments correspond to the atom number of the attached atom before the bond was cleaved. 

At this point we can discard the acyclic fragments.  As a final cleanup step, we'll remove the atom labels and replace the dummy atoms with hydrogen atoms.  This leaves us with two fragments that represent the two ring systems in our input molecule. 

There are other approaches to identifying ring systems that would treat the molecule above differently.  In the 2022 paper by Chen mentioned above, this molecule would be considered to have three ring systems. 

This approach requires the introduction of "extra" atoms to terminate the double bond between rings.  This felt somewhat artificial, and I decided to retain double bonds between rings.  To be honest, this a stylistic choice, and I think either approach could be considered valid. 

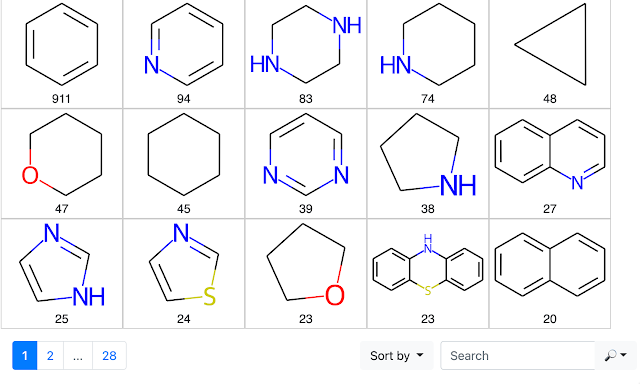
An Application of the RingSystemFinder

An implementation of the algorithm above is available in a Python class that is part of the latest release of my useful_rdkit_utils package.  This package can be installed with the command

pip install useful_rdkit_utils

As a demonstration of the method, I put together a Jupyter notebook to calculate the frequency of occurrence of ring systems in marketed drugs.  This workflow is similar to the approach used in the papers mentioned above that examine which ring systems are most commonly used in drug molecules.  The notebook shows how, with very little code, we can arrive at a nice table of chemical structures and associated statistics.   The notebook can be run on Google Colab without installing software locally.